Shepherd's Blog

2304. 网格中的最小路径代价

https://leetcode.cn/problems/minimum-path-cost-in-a-grid/description/

给你一个下标从 0 开始的整数矩阵 grid ，矩阵大小为 m x n ，由从 0 到 m * n - 1 的不同整数组成。你可以在此矩阵中，从一个单元格移动到 下一行 的任何其他单元格。如果你位于单元格 (x, y) ，且满足 x < m - 1 ，你可以移动到 (x + 1, 0), (x + 1, 1), …, (x + 1, n - 1) 中的任何一个单元格。注意： 在最后一行中的单元格不能触发移动。

每次可能的移动都需要付出对应的代价，代价用一个下标从 0 开始的二维数组 moveCost 表示，该数组大小为 (m * n) x n ，其中 moveCost[i][j] 是从值为 i 的单元格移动到下一行第 j 列单元格的代价。从 grid 最后一行的单元格移动的代价可以忽略。

grid 一条路径的代价是：所有路径经过的单元格的 值之和 加上 所有移动的 代价之和 。从 第一行 任意单元格出发，返回到达 最后一行 任意单元格的最小路径代价。

示例 1：

img

1
2
3
4
5
6
7
输入：grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]
输出：17
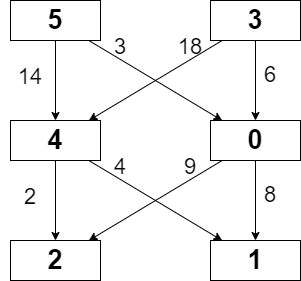
解释：最小代价的路径是 5 -> 0 -> 1 。
- 路径途经单元格值之和 5 + 0 + 1 = 6 。
- 从 5 移动到 0 的代价为 3 。
- 从 0 移动到 1 的代价为 8 。
路径总代价为 6 + 3 + 8 = 17 。

示例 2：

1
2
3
4
5
6
7
输入：grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]]
输出：6
解释：
最小代价的路径是 2 -> 3 。 
- 路径途经单元格值之和 2 + 3 = 5 。 
- 从 2 移动到 3 的代价为 1 。 
路径总代价为 5 + 1 = 6 。

提示：

  • m == grid.length
  • n == grid[i].length
  • 2 <= m, n <= 50
  • grid 由从 0 到 m * n - 1 的不同整数组成
  • moveCost.length == m * n
  • moveCost[i].length == n
  • 1 <= moveCost[i][j] <= 100

记忆化搜索

我们定义 $dfs(i,j)$ 表示到达 $grad[i][j]$ 的最小路径代价，可以得出：
$$
dfs(i,j) =
\begin{cases}
grid[i][j] &i=0\
min_{k=0}^{n-1}{dfs(i-1,k)+moveCost[grid[i-1][k]][j]+grid[i,j]} &i>0
\end{cases}
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public int[][] memo;

    public int dfs(int i, int j, int[][] grid, int[][] moveCost) {
        if (i == 0) {
            return grid[i][j];
        }
        if (memo[i][j] > 0) {
            return memo[i][j];
        }
        int ans = Integer.MAX_VALUE;
        for (int k = 0; k < grid[i - 1].length; k++) {
            ans = Math.min(ans, dfs(i - 1, k, grid, moveCost) + moveCost[grid[i - 1][k]][j] + grid[i][j]);
        }
        return memo[i][j] = ans;
    }

    public int minPathCost(int[][] grid, int[][] moveCost) {
        int m = grid.length;
        int n = grid[0].length;
        memo = new int[m][n];
        int ans = Integer.MAX_VALUE;
        for (int i = 0; i < n; i++) {
                ans = Math.min(ans, dfs(m - 1, i, grid, moveCost));
        }
        return ans;
    }
}

动态规划

将上一步的 $dfs(i,j)$ 改为 $dp[i][j]$ :
$$
dp[i][j] =
\begin{cases}
grid[i][j] &i=0\
min_{k=0}^{n-1}{dp[i-1][k]+moveCost[grid[i-1][k]][j]+grid[i,j]} &i>0
\end{cases}
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int minPathCost(int[][] grid, int[][] moveCost) {
        int m = grid.length;
        int n = grid[0].length;
        int[][] dp = new int[m][n];
        dp[0] = grid[0];
        for (int i = 1; i < m; i++) {
            for (int j = 0; j < n; j++) {
                dp[i][j] = Integer.MAX_VALUE;
                for (int k = 0; k < n; k++) {
                    dp[i][j] = Math.min(dp[i][j], dp[i - 1][k] + moveCost[grid[i - 1][k]][j] + grid[i][j]);
                }
            }
        }
        int ans = Integer.MAX_VALUE;
        for (int i : dp[m - 1]) {
            ans = Math.min(ans, i);
        }
        return ans;
    }
}
0%