Shepherd's Blog

1457. 二叉树中的伪回文路径

https://leetcode.cn/problems/pseudo-palindromic-paths-in-a-binary-tree/description/

给你一棵二叉树，每个节点的值为 1 到 9 。我们称二叉树中的一条路径是 「伪回文」的，当它满足：路径经过的所有节点值的排列中，存在一个回文序列。

请你返回从根到叶子节点的所有路径中 伪回文 路径的数目。

示例 1：

img

1
2
3
4
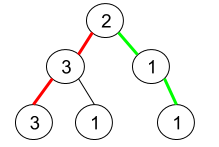
输入：root = [2,3,1,3,1,null,1]
输出：2 
解释：上图为给定的二叉树。总共有 3 条从根到叶子的路径：红色路径 [2,3,3] ，绿色路径 [2,1,1] 和路径 [2,3,1] 。
     在这些路径中，只有红色和绿色的路径是伪回文路径，因为红色路径 [2,3,3] 存在回文排列 [3,2,3] ，绿色路径 [2,1,1] 存在回文排列 [1,2,1] 。

示例 2：

img

1
2
3
4
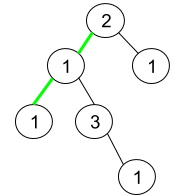
输入：root = [2,1,1,1,3,null,null,null,null,null,1]
输出：1 
解释：上图为给定二叉树。总共有 3 条从根到叶子的路径：绿色路径 [2,1,1] ，路径 [2,1,3,1] 和路径 [2,1] 。
     这些路径中只有绿色路径是伪回文路径，因为 [2,1,1] 存在回文排列 [1,2,1] 。

示例 3：

1
2
输入：root = [9]
输出：1

提示：

  • 给定二叉树的节点数目在范围 [1, 105] 内
  • 1 <= Node.val <= 9

深度优先遍历，当遍历至叶子节点时，判断当前路径上出现过数的次数，保证至多只有一个数出现过奇数次，则当前路径为伪回文路径。

使用数组缓存状态

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    int[] cache = new int[10];

    public int dfs(TreeNode node) {
        if (node == null) {
            return 0;
        }
        cache[node.val]++;
        int res = 0;
        if (node.left == node.right) {
            res = isPseudoPalindrome() ? 1 : 0;
        } else {
            res = dfs(node.left) + dfs(node.right);
        }
        cache[node.val]--;
        return res;
    }

    public boolean isPseudoPalindrome() {
        int odd = 0;
        for (int i : cache) {
            odd += i & 1;
        }
        return odd <= 1;
    }

    public int pseudoPalindromicPaths (TreeNode root) {
        return dfs(root);
    }
}

使用位缓存状态

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int pseudoPalindromicPaths (TreeNode root) {
        return dfs(root, 0);
    }

    public int dfs(TreeNode node, int mask) {
        if (node == null) {
            return 0;
        }
        mask ^= 1 << node.val;
        if (node.left == node.right) {
            return (mask & (mask - 1)) == 0 ? 1 : 0;
        }
        return dfs(node.left, mask) + dfs(node.right, mask);
    }
}
0%