https://leetcode.cn/problems/find-the-city-with-the-smallest-number-of-neighbors-at-a-threshold-distance/description/
有 n 个城市,按从 0 到 n-1 编号。给你一个边数组 edges,其中 edges[i] = [fromi, toi, weighti] 代表 fromi 和 toi 两个城市之间的双向加权边,距离阈值是一个整数 distanceThreshold。
返回能通过某些路径到达其他城市数目最少、且路径距离 最大 为 distanceThreshold 的城市。如果有多个这样的城市,则返回编号最大的城市。
注意,连接城市 i 和 j 的路径的距离等于沿该路径的所有边的权重之和。
示例 1:
1
2
3
4
5
6
7
8
9
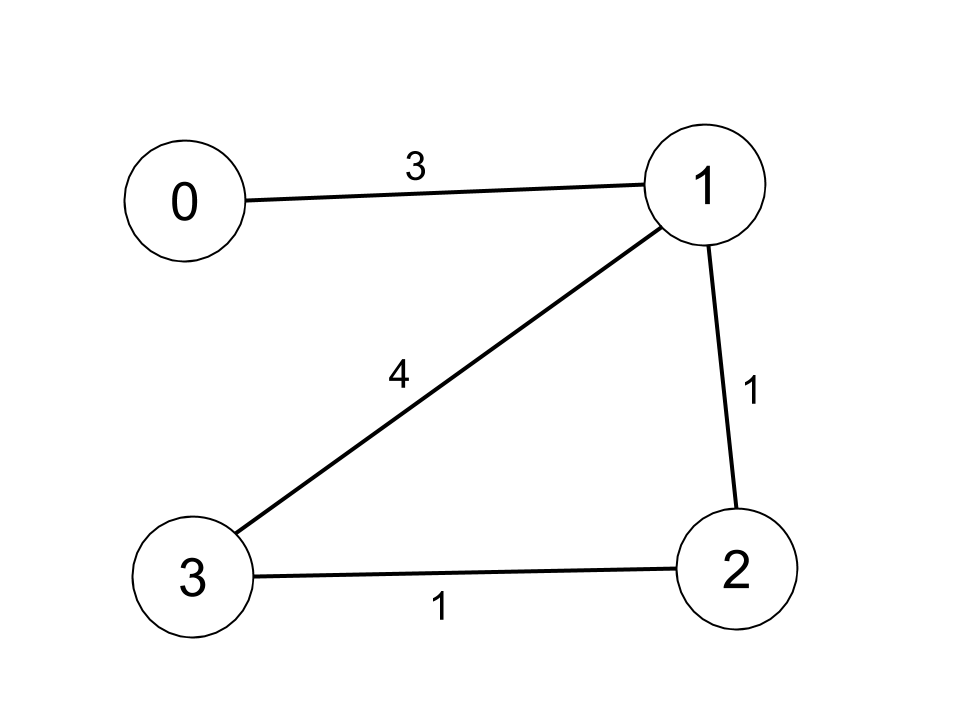
| 输入:n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
输出:3
解释:城市分布图如上。
每个城市阈值距离 distanceThreshold = 4 内的邻居城市分别是:
城市 0 -> [城市 1, 城市 2]
城市 1 -> [城市 0, 城市 2, 城市 3]
城市 2 -> [城市 0, 城市 1, 城市 3]
城市 3 -> [城市 1, 城市 2]
城市 0 和 3 在阈值距离 4 以内都有 2 个邻居城市,但是我们必须返回城市 3,因为它的编号最大。
|
示例 2:
1
2
3
4
5
6
7
8
9
10
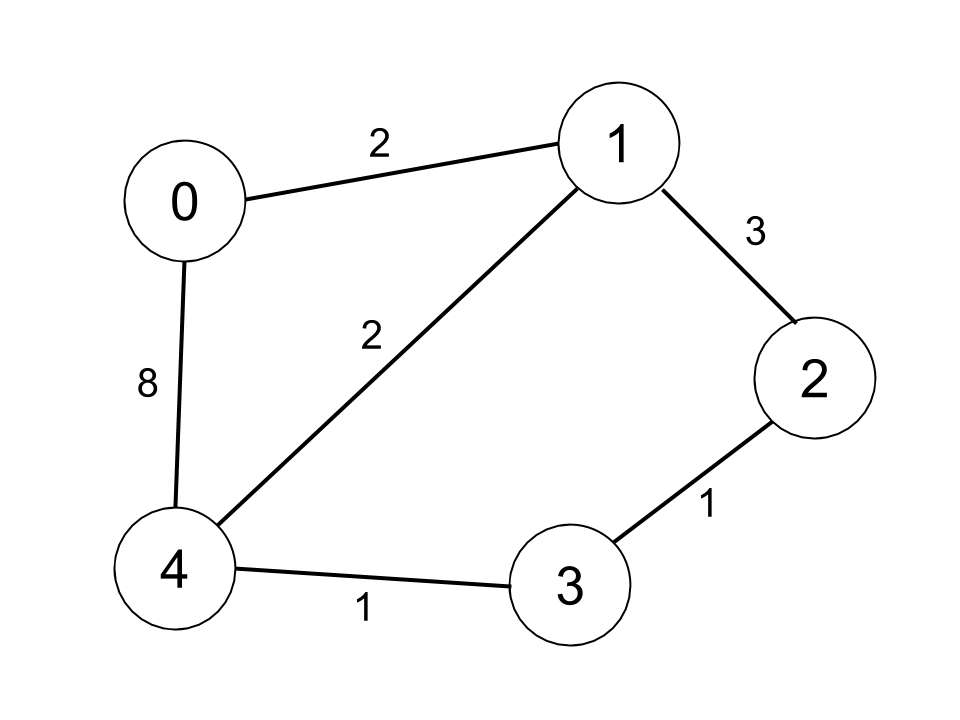
| 输入:n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
输出:0
解释:城市分布图如上。
每个城市阈值距离 distanceThreshold = 2 内的邻居城市分别是:
城市 0 -> [城市 1]
城市 1 -> [城市 0, 城市 4]
城市 2 -> [城市 3, 城市 4]
城市 3 -> [城市 2, 城市 4]
城市 4 -> [城市 1, 城市 2, 城市 3]
城市 0 在阈值距离 2 以内只有 1 个邻居城市。
|
提示:
2 <= n <= 1001 <= edges.length <= n * (n - 1) / 2edges[i].length == 30 <= fromi < toi < n1 <= weighti, distanceThreshold <= 10^4- 所有
(fromi, toi) 都是不同的。
递归(超时)
定义 $dfs(k,i,j)$ 表示从 $i$ 到 $j$ 的最短路径,并且这条最短路的中间节点编号都 $\le k$ 。
- 如果路径不经过 $k$ ,那么剩余的路径节点都小于 $k$ ,即 $dfs(k-1,i,j)$ 。
- 如果路径经过 $k$ ,那么问题分解为从 $i$ 到 $k$ 的路径与从 $k$ 到 $j$ 的路径,由于路径中不包含端点,即 $dfs(k-1,i,k)+dfs(k-1,k,j)$ 。
两种情况取最小值,即:
$$
dfs(k,i,j)=min(dfs(k-1,i,j),dfs(k-1,i,k)+dfs(k-1,k,j))
$$
递归边界:$dfs(-1,i,j)=w[i][j]$ , $w[i][j]$ 表示连接 $i$ 和 $j$ 的边的边权。
递归入口:$dfs(n-1,i,j)$ 。
作者:灵茶山艾府
链接:https://leetcode.cn/problems/find-the-city-with-the-smallest-number-of-neighbors-at-a-threshold-distance/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| class Solution {
public int findTheCity(int n, int[][] edges, int distanceThreshold) {
int[][] w = new int[n][n];
for (int[] row : w) {
Arrays.fill(row, distanceThreshold + 1);
}
for (int[] edge : edges) {
int x = edge[0];
int y = edge[1];
int wt = edge[2];
w[x][y] = w[y][x] = wt;
}
int res = 0;
int mincnt = n;
for (int i = 0; i < n; i++) {
int cnt = 0;
for (int j = 0; j < n; j++) {
if (j != i && dfs(n - 1, i, j, w) <= distanceThreshold) {
cnt++;
}
}
if (cnt <= mincnt) {
mincnt = cnt;
res = i;
}
}
return res;
}
private int dfs(int k, int i, int j, int[][] w) {
if (k < 0) {
return w[i][j];
}
return Math.min(dfs(k - 1, i, j, w), dfs(k - 1, i, k, w) + dfs(k - 1, k, j, w));
}
}
|
记忆化搜索
由于 $dfs$ 计算过程中会出现大量重复的计算过程,添加缓存存储已经计算过的结果,再次查询时直接返回即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| class Solution {
public int findTheCity(int n, int[][] edges, int distanceThreshold) {
int[][] w = new int[n][n];
for (int[] row : w) {
Arrays.fill(row, distanceThreshold + 1);
}
for (int[] edge : edges) {
int x = edge[0];
int y = edge[1];
int wt = edge[2];
w[x][y] = w[y][x] = wt;
}
int[][][] memo = new int[n][n][n];
int res = 0;
int mincnt = n;
for (int i = 0; i < n; i++) {
int cnt = 0;
for (int j = 0; j < n; j++) {
if (j != i && dfs(n - 1, i, j, memo, w) <= distanceThreshold) {
cnt++;
}
}
if (cnt <= mincnt) {
mincnt = cnt;
res = i;
}
}
return res;
}
private int dfs(int k, int i, int j, int[][][] memo, int[][] w) {
if (k < 0) {
return w[i][j];
}
if (memo[k][i][j] != 0) {
return memo[k][i][j];
}
return memo[k][i][j] = Math.min(dfs(k - 1, i, j, memo, w), dfs(k - 1, i, k, memo, w) + dfs(k - 1, k, j, memo, w));
}
}
|
递推
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| class Solution {
public int findTheCity(int n, int[][] edges, int distanceThreshold) {
int[][] w = new int[n][n];
for (int[] row : w) {
Arrays.fill(row, distanceThreshold + 1);
}
for (int[] edge : edges) {
int x = edge[0];
int y = edge[1];
int wt = edge[2];
w[x][y] = w[y][x] = wt;
}
int[][][] f = new int[n + 1][n][n];
f[0] = w;
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
f[k + 1][i][j] = Math.min(f[k][i][j], f[k][i][k] + f[k][k][j]);
}
}
}
int res = 0;
int mincnt = n;
for (int i = 0; i < n; i++) {
int cnt = 0;
for (int j = 0; j < n; j++) {
if (j != i && f[n][i][j] <= distanceThreshold) {
cnt++;
}
}
if (cnt <= mincnt) {
mincnt = cnt;
res = i;
}
}
return res;
}
}
|
Floyd-Warshall 算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| class Solution {
public int findTheCity(int n, int[][] edges, int distanceThreshold) {
int[][] w = new int[n][n];
for (int[] row : w) {
Arrays.fill(row, distanceThreshold + 1);
}
for (int[] edge : edges) {
int x = edge[0];
int y = edge[1];
int wt = edge[2];
w[x][y] = w[y][x] = wt;
}
int[][] f = w;
for (int k = 0; k < n; k++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
f[i][j] = Math.min(f[i][j], f[i][k] + f[k][j]);
}
}
}
int res = 0;
int mincnt = n;
for (int i = 0; i < n; i++) {
int cnt = 0;
for (int j = 0; j < n; j++) {
if (j != i && f[i][j] <= distanceThreshold) {
cnt++;
}
}
if (cnt <= mincnt) {
mincnt = cnt;
res = i;
}
}
return res;
}
}
|

